Here I want to break down a non electro-vacuum (EV) metric which I chose to contribute to the geodesic function in einsteinPy: Reissner-Nordström metric.
[edit: When initially writing this I believed Reissner-Nordström metric was a non EV metric, but later on as discovered in my blog I realised that it is an EV metric instead, please note that the rest of this research is correct and has been overseen]
Here I want to understand the metric equation, identify any variables used, define the metric function and how I would implement it into the code.
Before we delve right into the metric, I think it’s important we look into other definitions and solutions.
Geodesics is a length-minimising curve that shows the path a non-accelerating particles (or light particles) follows. It is part of Einstein’s theory of general relativity. (Busemann, 2012)
The Schwarzschild solution lays the foundation of general relativity, providing an exact solution to Einstein’s vacuum equations. It talks about the geometry of spacetime from a non-rotating, uncharged massive object, commonly associated with black holes. (Wikipedia Contributors, 2019)
Now, let’s delve into the Reissner-Nordström metric – this is like the older sibling to the Schwarschild metric, as it also includes electrical charge and rotation. It can explain Einstein’s equation to the behaviour behind space and time around a charged spinning object. This all means that electromagnetism is present here, not just gravity.(DIVA, n.d.)
When an object is charged and spinning, it can no longer be a perfectly spherical shape, the formula of the Reissner-Nordström proves this. The same method can be utilised to derive the Kerr-Newman metric, not just the Schwarschild metric, which takes the calculations of charge and rotation to a next level.
Let’s break down the metric equation, identify its variables, and define the metric function:
The formula for the Reissner-Nordström metric mainly involves variables such as mass (M) and electric charge (Q).
For more detail I have displayed the full formula and list of what everything in this expression represents.

The images here were collected from wikipedia, it displays the formula, as well as what each variable is:
- c is the speed of light
- Tau represents the proper time.
- t is the time coordinate
- r is the radical coordinate
- Theta and phi are the spherical angles
- The Schwarzchild radius formula is included, its formula is displayed below.
- rQ is the characteristic length scale, it formula is also presented
- Q is the electric constant.
(Wikipedia, 2021)
Below I wanted to add a modified version of the formula, here there isn’t terms for mass or charge like the Reissner-Nordström metric does. This is more similar to Schwarzschild metric.
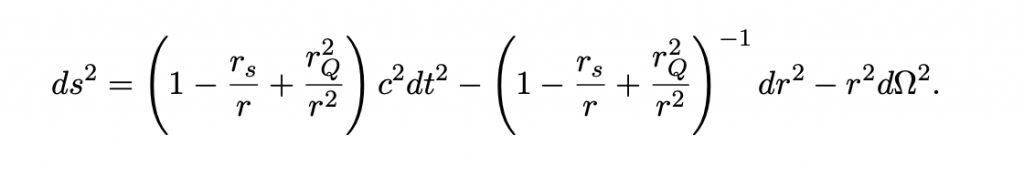
- c is the speed of light
- t is the time coordinate
- r is the radical coordinate
- dΩ2 is the angular part of this metric, often shown with angular coordinates like dθ2+sin2θ dϕ2dθ2+sin2θdϕ2 in spherical coordinates.
- rQ is the characteristic length scale
- Q is the electrical charge
In conclusion, through this process I have deepened my understanding of the metric equations and the variables involved, such as mass (M) and charrge (Q). I briefly explored the basics of geodesics and the Schwarzschild solution, which the Reissner-Nordström metric is an extension of this.
Contributing towards this issue with better knowledge on the topic benefits my potential with this project, and I look forward to contributing toward this issue and engaging with its community.
References:
Busemann, H. (2012). The Geometry of Geodesics. [online] Google Books. Courier Corporation. Available at: https://books.google.co.uk/books?hl=en&lr=&id=DOdx1FPmGNMC&oi=fnd&pg=PP1&dq=geodesics&ots=RwmdkicUAZ&sig=njC97a-Kgrp-3jYlzWo_olSCxoQ&redir_esc=y#v=onepage&q=geodesics&f=false [Accessed 10 Jun. 2024].
DIVA. (n.d.). http://www.diva-portal.org/smash/record.jsf?pid=diva2%3A912393. [online] Available at: https://www.diva-portal.org/smash/record.jsf?pid=diva2%3A912393&dswid=-6200/ [Accessed 10 Jun. 2024].
Wikipedia Contributors (2019). Schwarzschild metric. [online] Wikipedia. Available at: https://en.wikipedia.org/wiki/Schwarzschild_metric.
Wikipedia (2021). Reissner–Nordström metric. [online] Wikipedia. Available at: https://en.wikipedia.org/wiki/Reissner%E2%80%93Nordstr%C3%B6m_metric.